In this post I model the reference sequence U00096.3 of Escherichia coli strain K-12 using Markov models and simple neural networks. The goal is to try predict to the nucleotide in some position of the genome, given some number of preceding nucleotides as a context.
Let’s start with some basic statistics. There are 4.6 million nucleotides in the genome. All four nucleotides are approximately equally common:
| A | C | G | T |
| 24.62% | 25.42% | 25.37% | 24.59% |
Guessing nucleotides randomly always gives a prediction accuracy of 25%. We can improve to 25.42% by always guessing the most common nucleotide C. One way to try to improve on this is to use a Markov model.
Markov models
In our setup, a Markov model of order k is a model that predicts the next nucleotide in a sequence based only on the k previous characters of the sequence. The k previous characters are called the context. The model learns a probability distribution for the next nucleotide for each of the 4^k possible distinct contexts. We can take the most likely nucleotide in the distribution as the prediction of the model.
For example, a Markov model of order 2 would have 16 contexts: AA, AC, AG, AT, CA, CC, CG, CT, GA, GC, GG, GT, TA, TC, TG and TT. Each of these would be associated with a probability distribution over A, C, G and T. For example, for the context TG, we could have P(A | TG) = 0.2, P(C | TG) = 0.1, P(G | TG) = 0.5, P(T | TG) = 0.1. This model would predict that if the context is TG, the next nucleotide is most likely G.
The distributions for each context can be easily estimated from the reference genome. We can simply find all occurrences of a context, and see what distribution of characters are followed by the context in the data. If a context does not occur at all in the training data, we assume a uniform distribution.
To evaluate how well this works, I build a training dataset and test dataset. I put 50% of the positions in the reference genome to the training set, and the rest to the test set. The distributions are estimated from positions in the training dataset, and then the model tries to predict the nucleotides in all positions of the test set. I repeat this experiment for all possible Markov model orders from 0 to 16.
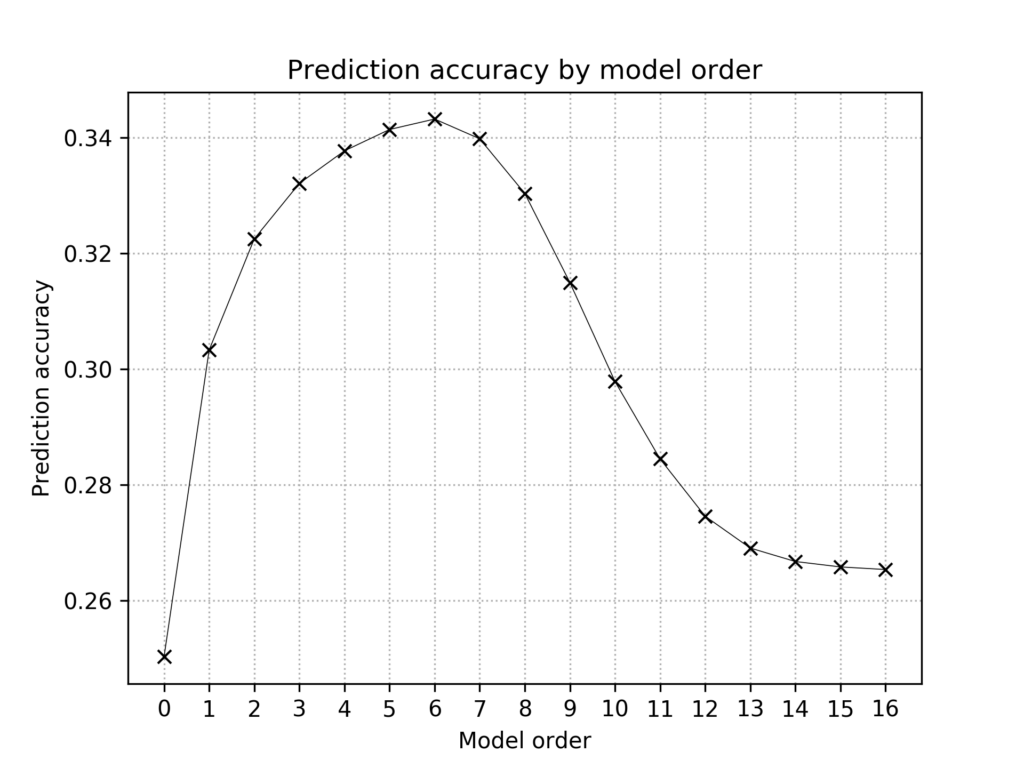
The best model turns out to have order 6, with an accuracy slightly above 34%. Models with a smaller degree are too coarse (underfitting), whereas models with a larger degree are too specific (overfitting).
Neural networks
If we increase the order of Markov model too much, the contexts are so specific that almost all of them will occur only once in the genome, and hence we can not estimate a reasonable distribution for the next nucleotide. However, there could be longer-range dependencies in the nucleotide sequence than what a low degree Markov model can exploit.
Neural networks are one possible way to try to exploit longer-range dependencies. The input to the network can be a context of any length, and the output will be a distribution for the next nucleotide.
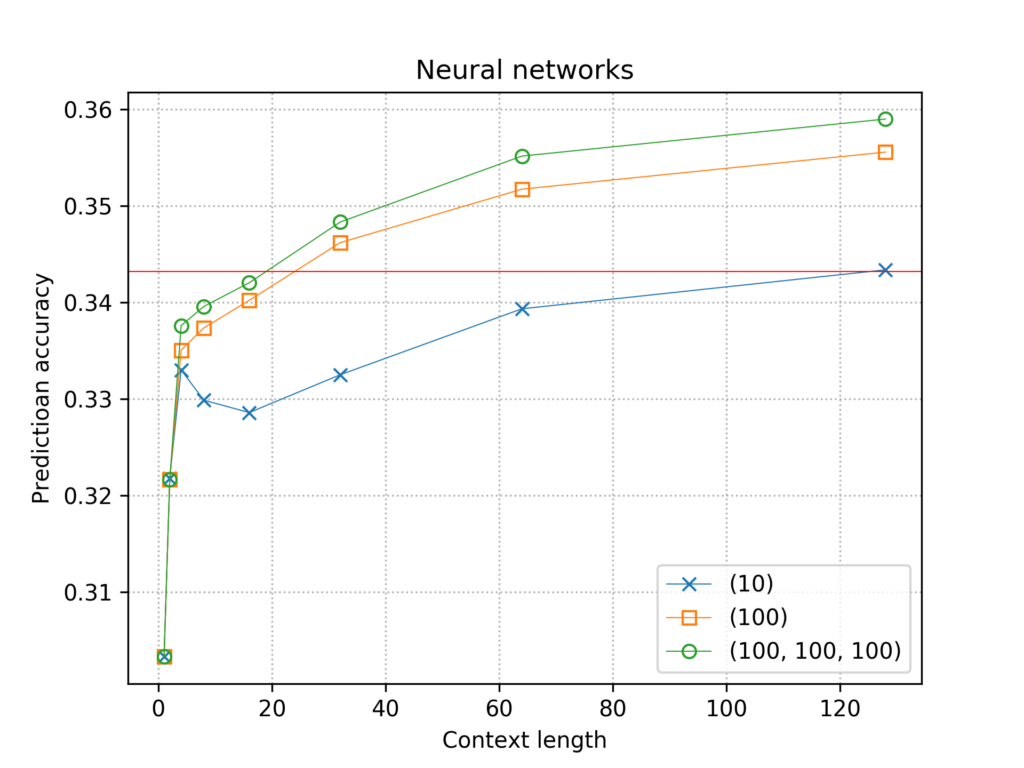
I tried three simple architectures. All three take as an input a one-hot encoded representation of the context, and output a distribution for the four nucleotides using a final softmax layer of size 4. The first and second architecture have a single hidden layer with 10 and 100 neurons respectively. The third architecture has three hidden layers of 100 neurons each. All layers are fully connected. I trained models in Tensorflow 2.0 with context lengths 1,2,4,8,16,32,64 and 128, with one full pass through the training data, using the default Adam optimizer and the categorical cross-entropy loss function. The final accuracies on the test set are plotted below. Each line corresponds to one hidden layer architecture. The red horizontal line shows the accuracy of the best Markov model.